My primary source for the physics of this comparison is a series of popular lectures by Richard Feynman, published in QED: The Strange Theory of Light and Matter. [1] Feynman was a primary architect of Quantum Electrodynamics (QED) and was its advocate as the most thorough and profound of current physical theories. He approached his theme through a discussion of the reflection of light from a surface. Reflection is a familiar phenomenon generally believed to be well understood by educated laymen, both in terms of common sense (" the angle of reflection equals the angle of incidence" ) and at the academic level of classical physical theory. Feynman's analysis shows that classical theory does not account adequately for the phenomena known today; it even reveals what one might call " mysteries" unsolvable except through quantum analysis. Furthermore, the interpretation in terms of quantum electrodynamics permits directly the progressive deepening of layers of analysis to the level of atomic particle interactions.
There is a dilemma in classical electrodynamics. Light is both a wave and a particle. Evidence for the wave- like character of light is first, interference phenomena where light from two sources cross; and second, the diffraction of light when passing through very small holes or slits. These experimental results, refined over hundreds for years from the time of Newton's original experiments, have been explainable only by the equations for waves interacting and " canceling out." The wave theory broke down in modern times when devices were developed sensitive enough to detect a single particle of light, a " photon." The wave theory predicted that the " clicks" of a detector would get softer as the light got dimmer, whereas the " clicks" actually stayed at full strength but occurred less frequently. No reasonable model could explain this fact. Feynman claims that quantum electrodynamics explains the phenomena of " wave- particle duality" without claiming to actually " resolve" the dilemma, that is, to reduce the explanation of the phenomena to an intuitive model based on experience in the everyday world. His description of this " resolution" characterizes his effort as typical of the practice of physics today:
" ...The situation today is, we haven't got a good model to explain partial reflection by two surfaces; we just calculate the probability that a particular photomultiplier will be hit by a photon reflected from a sheet of glass. I am going to show you " how we count the beans" - what the physicists do to get the right answer. I am not going to explain how the photons actually " decide" whether to bounce back or go through; that is not known. (Probably the question has no meaning.) I will only show you how to calculate the correct probability that light will be reflected from glass of a given thickness, because that's the only thing physicists know how to do! What we do to get the answer to this problem is analogous to the things we have to do to get the answer to every other problem explained by quantum electrodynamics... "
QED, Introduction, p. 24

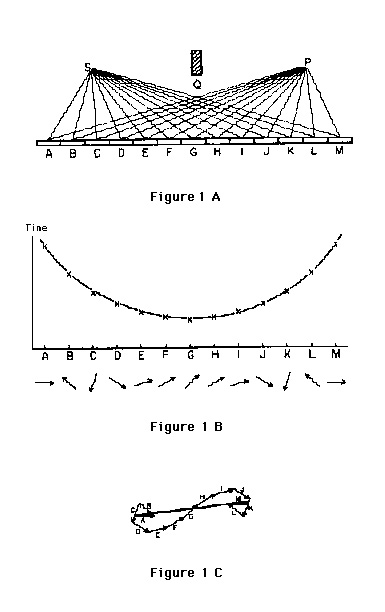
What determines how long the final arrow is? Notice a number of things. First, the ends of the mirror are not important: there, the little arrows wander around and don't get anywhere. If one chopped off the ends of the mirror, it would hardly affect the length of the final arrow. The part of the mirror that gives the final arrow a substantial length is the part where the arrows are all pointing in nearly the same direction — because their time to reach the photomultiplier is almost the same. The time is nearly the same from one path to the next at the bottom of the curve, where the time is least. Feynman concludes:
" ...To summarize, where the time is least is also where the time for the nearby paths is nearly the same; that's where the little arrows point in nearly the same direction and add up to a substantial length; that's where the probability of a photon reflecting off a mirror is determined. And that's why, in approximation, we can get away with the crude picture of the world that says that light only goes where the time is least... " So the theory of quantum electrodynamics gave the right answer—the middle of the mirror is the important part for reflection—but this correct result came out at the expense of believing that light reflects all over the mirror, and having to add a bunch of little arrows together whose sole purpose was to cancel out. All that might seem to you to be a waste of time—some silly game for mathematicians only. After all, it doesn't seem like " real physics" to have something there that only cancels out ! ... "
The virtue of machine learning studies is that they allow us no miracles; they can completely and unambiguously cover some examples of learning with mechanisms simple enough to be comprehensible. Must we claim that learning happens in people the same way? Not necessarily. Building such models is an exploration of the possible, according to a specification of what dimensions of consideration might be important. The computer's aid in systematically generating sets of all possible conditions helps liberate our view of what possible experiences might serve as paths of learning. Feynman asked what happened at all those other places on the reflecting surface where " the angle of reflection" doesn't equal " the angle of incidence." Similarly, when we can generate all possible interactions through which learning might occur—including some we first imagine are not important, we can explore those alternate paths and the suite of relationships among elements of the ensemble.
Strategies for achieving specific forks are the knowledge structures of SLIM. Each has three parts: a Goal, a sequence of Actions, and a set of Constraints on those actions (each triple is thereby a GAC). I simulated operation of such structures in a program that plays tic- tac- toe against variations of REO. Applying these strategies leads to moves that often result in winning or losing; this in turn leads to the creation of new structures, by specific modifications of the current GACs. The modifications are controlled by a small set of rules, so that the GACs are interrelated by the ways modifications can map from one to another. [6]
In order to evaluate specific learning mechanisms in particular cases, one must go beyond counting outcomes; one must examine and specify which forks are learned from which predecessors in which sequence and under which conditions of opponent cell preferences. The simulation avoided abstraction, in order to explore learning based on the modification of fully explicit strategies learned through particular experiences. [7] The results are first, a catalog of specific experiences through which learning occurs within this system and second, a description of networks of descent of specific strategies from one another. The catalog permits a specification of two desired results: first, which new forks may be learned when some predecessor is known; and second, which specific interaction gives rise to each fork learned. The results obviously also depend on the specific learning algorithm used by SLIM.
Consider how SLIM can learn the symmetrical variation to one particular fork. Suppose that SLIM begins with the objective of developing a fork represented by the Goal pattern {1 3 9} and will proceed with moves in the sequence the plan [1 9 3] (see figure 2). SLIM moves first to cell 1. REO prefers the center cell (5), and moves there. SLIM moves in cell 9. The plan is followed until REO's second move is to cell 3. [8] SLIM's plan is blocked. The strategic goal {1 3 9} is given over -- but the game is not ended. SLIM, now playing tactically with the same set of rules as REO, moves into cell 7, the only remaining corner cell. Unknowingly, SLIM has created a fork symmetrical to its fork- goal. SLIM can not recognize the fork. It has not the knowledge to do so. What happens ? REO blocks one of SLIM's two ways- to- win, choosing cell 4. SLIM, playing tactically, recognizes that it can win and moves into cell 8. This is the key juncture.
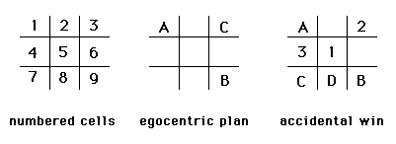
SLIM recognizes " winning without expecting to do so" as a special circumstance. Even more, SLIM assumes that it has won through creating an unrecognized fork (otherwise REO would have blocked the win). SLIM takes the pattern of its first three moves as a fork. That pattern {1 7 9} is made the goal of a new GAC. SLIM examines its known plans for creating a fork (there is one, [1 9 3]) with the list of its own moves, executed in sequence before the winning move was made [1 9 7]. The terminal step of the plan is the only difference between the two. SLIM modifies thprototype plan terminal step to create a new plan, [1 9 7]. SLIM now has two GACs for future play. [9]
The complete set of results involves consideration of all paths of possible learning, even those deemed unlikely a priori, and concludes with the complete specification of all possible paths of learning every fork given any fork prototype. Consideration of all paths of learning I take to be comparable to consideration of all paths over which photon might travel when striking a surface. For corner opening play, the first six GACs form a central collection of strategies. Their interrelations can be represented as trees of derivation or descent (as shown in Figure 3).
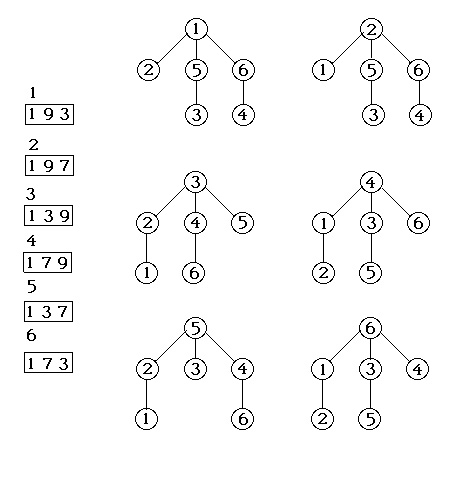
The tree with strategy three as top node may be taken as typical. Play in five specific games beginning with only GAC 3 known, generates the other five central GACs. The specialness of the six central nodes is a consequence of their co- generatability. Some of those are directly generatable, can generate each other (such as GACs 1 and 2) ; they are reciprocally generatable. Some lead to each other through intermediaries (such as GAC 1 and 3); they are cyclically generatable. For these six central strategies, the trees of structure descent can fold together into a connected network of descent whose relations of co- generativity are shown in Figure 4.
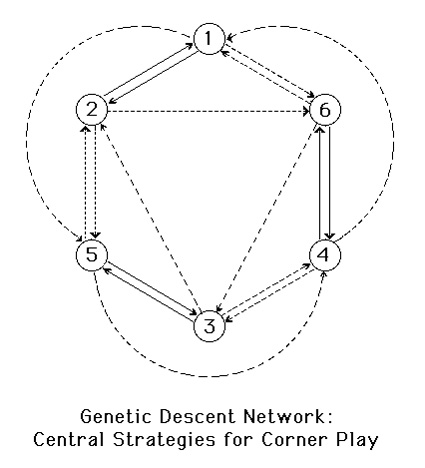
The form of these descent networks is related to symmetry among forking patterns. But they include more: they reflect the play of the opponent, the order in which the forks are learned, and the specific learning mechanisms permitted in the simulations. These descent networks are summaries of results.
There are many paths of possible learning, some central and some peripheral. In QED, the criterion of centrality is near- uniform directionality of the photon arrows. In SLIM, the criterion of centrality is a different and a new one: co- generativity. The basic method is to aggregate results of all possibilities in a fully explicit manner. The process of aggregation is where the differences become systematic and significant. In QED, the aggregation of individual results is formally analytic—that is the solution of path- integral equations of functions of complex variables . In SLIM, one begins with lists of games won without a plan. One then reformulates the relations between prototypes and generated plans into trees of fork plan transformations, which are the trees of descent. The learning algorithms are the functional mechanisms effecting the transformations. In the analysis of SLIM, aggregation is systematic and constructive though not formal: one pulls together the empirical results of exhaustive exploration (trees of descent in figure 3) into a new representation scheme (the genetic networks of descent in figures 4).
In general, the process followed with these data is similar to Weyl's use of reformulation in his general description of the development of theoretic knowledge in Symmetry and Bourbaki's description of the genesis of axiomatic systems in The Architecture of Mathematics. Working with SLIM started with the general principle that learning happens through interaction. The model was constructed to represent the behavior of both the learner and the opponent in explicit detail with specification of representations and learning algorithms giving the notion a precise meaning. Through the aggregation and reformulation of results, a new generality was achieved which suggested a new idea - - that co- generatability of related but variant knowledge forms is what makes learning possible in any particular domain. This principle would support stable knowledge in minds with reconstructive memories, such as Bartlett (1932) suggests humans have.
Furthermore, of course, QED claims completeness in covering all known interactions of photons and electrons. Strategy learning is important, but not so fundamental in cognition as electron- photon interactions are in physics. Moreover, quantum electrodynamics permits going further down in detail to the discussion of interactions of such particles in the matter.
In respect of ways for aggregating results, the similarities are superficial unless the consequences are similar or significant for some other reason. What are the results of Feynman's analysis? Two results at least are important in their use for us. Feynman says that one must regularly remind students of the goal of the process—discovering " the final arrow," that is, the resultant vector of probability amplitudes, and understanding how the particularities of the interaction generate that " final arrow." Our objective is comparable. The learnability analysis of this paper introduces two novelties: a new goal and a new principle. The new goal transforms a psychological focus to an epistemological one. At this point one is not so much interested in what a particular child did as an individual. But the case provides some boundary conditions for modeling with the question " if the details of at least one natural case have such characteristics, what kinds and paths of learning are possible?" [10] The question is of general interest if one admits that particularity and egocentricity are common characteristics of novice thought.
Where Feynman's analysis of reflection depends on the principle of least time to determine what paths contribute most to the observable " final arrow," SLIM points to co- generativity, represented by those connections in the central group (strategies 1- 6) permitting each one to be learned no matter which is adopted as the prototype fork. Peripheral strategies [11] are rarely learned because they can be learned in few ways. The conclusion is that one can characterize the learnability of a domain as a function of particular interactions among agents based on the connectedness of possible paths of strategy learning. This is what the network of genetic descent does. That network is the equivalent of the " final arrow" of Feynman's analysis of reflection, despite its different appearance and different basis. Furthermore, these methods and representations reveal what makes it possible to learn in a problem domain; even what makes it possible to judge that knowledge of a given domain is more learnable in one context than in another. The new principle is that the learnability of a domain is the result of all the possible cases of concrete learning through particular experience; those that contribute significantly to the learnability of a domain are those that are mutually reinforcing, in the sense that they are co- generative: A - > B - > C - > A, etc. This is directly comparable to what one finds the case in addition of arrows - - the final effect results from the aggregation of related components; isolated possibilities don't add up to a significant result. The new principle - - identifying the learnability of a domain with its connectedness - - is a direct consequence of the state transformations being the learning algorithms of the system. One may paraphrase the situation thus: you'll learn where Rome is, if all roads lead there.
Whitehead noted that the value of a formalism is that it lets you apply a practical method without concentrating too much on it; so that one's attention can be given to inventing and applying methods to other problems. Knowing how to add, for example, permits us to ignore the process and to focus on the meaning or significance of elements operated on. Whitehead asserted the same is true for the calculus. It is also is important for models such as SLIM—which generates dependably a list of all relevant games playable given a prototype strategy. That list can be filtered to permit focus on some subset of games of high interest—such as those won by the player. Computational procedures are formal, but modeling as an activity is more constructive than analytic. That may make it more apt for representing what we know of learning than analytic methods. Finally, even if one cannot explain human learning at a comparable level to that at which one can explain reflection:
* Given that the principle that co- generativity under specific algorithms provides the explanation of differential learnability, one should be able to articulate why learning is possible in specific domains on the basis of the internal relationships of schemes of representations and learning algorithms, the latter seen as transformations between the states of those relationships.
This is a retreat from the Lewin's psychology of the pure case to epistemology. Others have retreated before us and still made a contribution, as physicists did in order to " resolve" the wave- particle duality.
Throughout this paper, the issue of whether or not simple descriptions can comprise " real science" has continually surfaced. Different people have different criteria for judging what work is scientific and what is not. Peirce, for instance, argued that science is defined by a question of intent (generally based on a real objective of finding out what is the case in the world) and that method is derivative though still significant. Exploring epistemology through computation is clearly scientific in intent (thus, by Peirce's criterion). It is also arguably scientific in method, as marked by its similarity to Feynman's explication of QED. One should ask of such work not " is it science?" as judged by some narrow criterion, but " is it good science? Is it important science?" Ultimately, that judgment must be made on the merits of the particular case.
References and Acknowledgements
Publication notes: